Measurement type Dispersion
The purpose of measures of dispersion is to find out how to spread out the data values are on the number line.
The range of a set of data is the difference between the largest and smallest values
Range = Maximum value - Minimum value
| Range = 39-9 =30 |
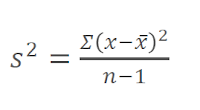 |
| Sample variance |
 |
| population variance |
1.Calculating the Sample variance for the values: 4, 7, 8,9, 11
We have to find mean for the following values : 4 + 7 + 8 + 9 + 11 / 5 = 39 / 5
Mean = 7.8
S^2 = (4-7.8)^2 + (7-7.8)^2 + ( 8-7.8)^2 + (9-7.8)^2 + (11-7.8)^2 / 5-1
= 6.7
Therefore, the sample variance is 6.7
STANDARD DEVIATION is a measure that is used to quantify the amount of variation or dispersion of a set of data values
we can find standard deviation by adding square root to variance
we will get zeros if you won't square them
Population Standard Deviation:
PS = {4 , 7 , 8 ,9 ,11}
mean = 7.8
SAMPLE STANDARD DEVIATION:
Mean= 7.8
= sqrt(6.7) =2.59


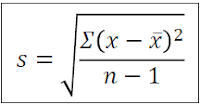

Very usefull blog for beginners!!
ReplyDelete